Advanced Conversion Tips: Analysis, Action & Attribution for 567% ROI

The dream is a familiar one…
Every ecommerce store owner dreams of growing their online store to rival all the big names out there. I am sure every one of us wants to have thousands of customers daily, millions in revenue, and a feature on the cover of Fortune’s “Fortune 500” issue.
All you need to achieve to get there? Consistently increasing revenue.
It sounds so simple when you say it, but the actual process of growing a company, as we all know, is a little more complicated.
Not only do you have to take care of daily operations — stocking items, arranging shipping, sourcing the best prices, etc. — you also need to be flexible enough to adjust to your customers’ expectations and anticipate their needs.
As if that’s not enough on your plate, you’re also expected to outsmart your competition (and they’re trying to do the same to you).
No wonder 7 out of 10 businesses fail in their first 10 years.
Ecommerce differs from other types of businesses in many key aspects. Most important is the customer’s physical disconnect from their purchased items — this is the gap we need to bridge. Simply bringing more visitors to the site will not result in a measurable improvement, unless the site copy and content foster trust and persuade potential customers to buy.
While methods to bring more traffic to an ecommerce site are very much the same as in traditional retail, the content needs to be different. CRO’s objective is to understand what content and persuasion customers need in order to be willing to buy, and how to further a website’s ultimate objective: growth.
To achieve revenue growth, CRO focuses on providing a better user experience, offering more relevant and engaging content, and increasing visitors’ motivation — not simply bringing more people to the site.
So, let’s start from the beginning.
What is conversion rate optimization (CRO)?
This guide is intended for everyone who needs to improve the performance of their website in order to increase revenue. Increasing revenue is the primary concern of conversion rate optimization, and it is an activity best suited for ecommerce websites.
Let’s start at the beginning with an explanation of the idea behind conversion rate optimization, and the definition of a few basic terms.
First: what is “conversion” and the “conversion rate”?
In ecommerce, “conversion” refers to the moment when a visitor to a site becomes a customer — they exchange money for a product or a service the site provides.
This is the ultimate purpose of every revenue-generating site out there, and it’s the only way for those sites to maintain their existence. While it is possible to make money just by driving traffic to your website, this is increasingly becoming an unsustainable business model.
Mathematically speaking, the conversion rate is the proportion of website visitors who end up converting out of the number of total visitors.
For example, if a website has regular traffic of 100,000 visits per month and 1,250 transactions per month, its conversion rate is 1.25%. Increasing that rate is the sole aim of conversion rate optimization.
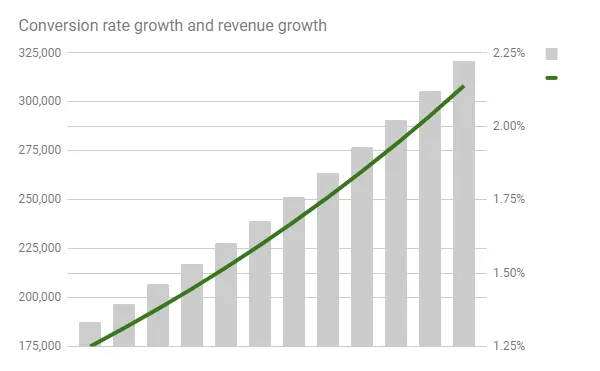
A graph depicting an increase in conversions from 1.25% with 100.000 visitors and average order value of 150$
If all other factors remain the same, by increasing its conversion rate, a site’s revenue will go up. “Other factors” here include the assumption that the number of visitors and the product prices will remain the same.
Obviously, it’s possible to increase conversions up to 100% if you offer your products for free — which will soon bankrupt you. You could also increase your conversion rate to 100% if you had only one visitor (for example, your spouse) who buys your product.
These are probably not the methods you’d prefer to use to increase your conversion rate.
The point of the entire exercise is to increase revenue by making a website’s performance objectively better (more responsive to customer needs, offering consistently engaging content) while relying upon its existing customer base.
Conversion rate optimization (CRO) methods are diverse. They range from technical analysis of a website to researching the opinions of your customers and the wider market. CRO digs into many fields, including:
Statistics
Marketing
Web development
User interface design
All of this is to achieve its goal: increasing the probability that any random visitor to a website will purchase a product sold there.
And CRO isn’t just applicable to ecommerce. Non-commercial and non-direct-revenue-generating websites can benefit from conversion optimization. CRO isn’t free, though, so if you depend on creating positive ROI, you may see negative net effects from spending money to optimize a site that’s not directly generating revenue.
In essence, CRO aims to make your existing customers more likely to buy, more often, and spend more when they buy. It also aims to make new visitors more likely to become your customers.
The process can be visually represented like this:
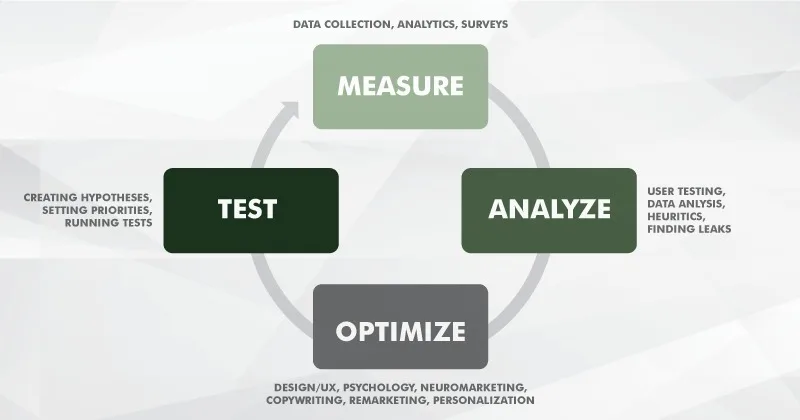
How to increase your conversion rate
There are many approaches to increasing conversion rate, but most of them have one thing in common: increasing the attractiveness of your website or offer, so more visitors decide that your offer is good enough for them.
Multiple factors influence the attractiveness of your overall offer. Some act as motivators or nudges, while other act as impediments or obstacles.
An example of a motivating factor is social proof. By improving social proof in the form of favorable reviews, testimonials, or case studies, you can influence the likelihood that any new visitor will convert.
How do you GET reviews and other social proof? Ask for it. You can incentivize your customers to provide you with social proof in various ways, so that you have more to show on your site, and more detailed accounts of how your product helps your customers.
Conversely, you need to reduce or minimize impediments in order to spur customers to convert. For example, some customers may find your shipping prices prohibitively expensive. While there is not much that an ecommerce store can do to influence the cost of shipping, it’s possible to offer new customers a discount to offset their shipping costs, or to offer free shipping for orders over some predetermined value.
The task of CRO is to identify all these factors, understand their role in how the site performs, find explanations for their effect, and propose solutions to enhance motivators and minimize impediments.
Time, cash, and reliability: When does it make sense to focus on CRO?
Focusing on conversion rate optimization makes sense for every website that derives a majority of its revenues via conversion. For these businesses, improving the conversion rate automatically brings in higher revenue.
But CRO does come with qualifiers that limit its application. Before going into the details, let’s talk about what it takes to properly conduct CRO.
1. Like every other business activity, CRO requires some investment to deliver benefits.
The first limitation of CRO is that it can cost a significant amount to conduct research, use tools, and pay researchers. Cost in monetary terms here refers to financing the cost of conducting the research, the cost of tools necessary to gather data and run experiments, and additional miscellaneous costs (such as incentivizing customers to provide feedback).
Depending on the intensity of work, costs can run upward of several tens of thousands of dollars for complete research.
When calculating the ROI delivered by CRO, always take into account that CRO activities reflect the entire spectrum of traffic acquisition. Increasing the relevance and performance of PPC ads, for example, will result in increased ROI from that source, but that increase won’t be directly attributable to CRO.
2. Properly conducted CRO research requires time.
Despite what you might have heard, CRO is not a silver bullet that will solve all your issues overnight. In fact, it frequently takes a month or more to just conduct research and gather data.
In most cases, you’re looking at six months to a year to establish a properly conducted CRO process. However, you’ll notice that even when “complete,” the CRO process compels you to continue putting in effort.
The third and final point limiting the application of CRO on every website is that the CRO methodology and research process relies on a sufficiently large amount of data.
In fact, without at least 100,000 visitors a month and at least 1,000 conversions in that time, there is not much point in conducting CRO. Without enough data, you cannot be confident that the patterns you spot in your research represent true trends.
Without enough data, you cannot be confident that the patterns you spot in your research represent true trends.
Having enough data is also essential for A/B testing, which is a major part of CRO. A/B testing depends on having a large enough sample to reach statistically significant results. Without enough visitors, it won’t be possible to prove any hypothesis.
Before you plunge headlong into CRO, remember to do the appropriate calculations. Your math needs to show that investing in CRO can produce a return on investment equal to, or larger than, other methods for increasing revenue — such as product improvements or increasing traffic through SEO, paid ads, or content marketing.
If your SEO strategy works great, and brings an ever-increasing number of visitors to your website at an acceptable cost, you may feel no need to engage in CRO. This decision makes sense.
After all, if everything is working smoothly, why try to fix it?
In this case, spending additional money (and time) on CRO will probably not be your first choice. However, you should be aware that the law of diminishing returns affects everything — your marketing spend included.
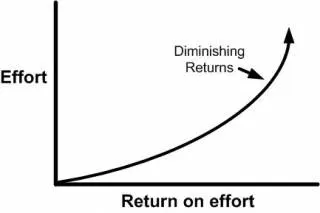
More trying for less cash over time
As you increase your expenditure on traffic acquisition, you will inevitably hit the point where each additional dollar you spend returns less than the previous one.
If you judge that your ad spend has reached its maximum possible effect, it’s time to start investing in CRO, which can also support your other marketing efforts.
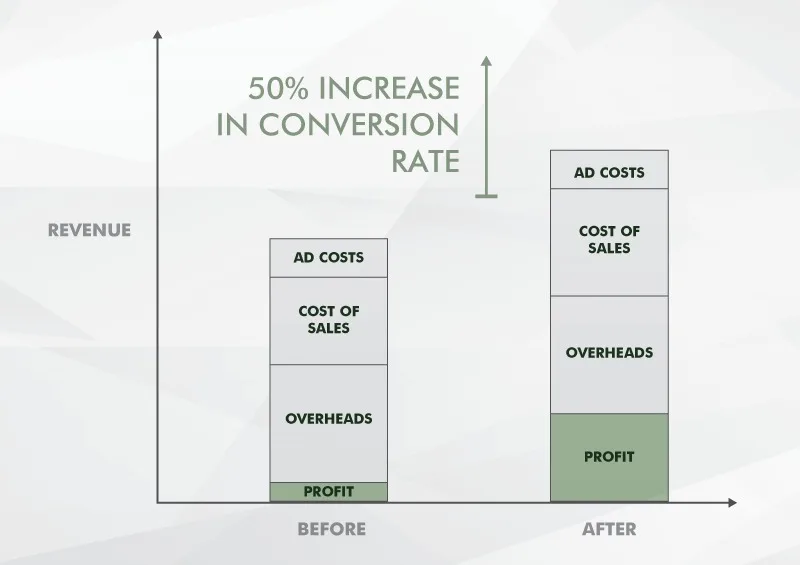
CRO complements all your marketing efforts
As you can see, when you increase your conversion rate by 50%, with all other costs staying the same, you’ll generate more profit to dedicate to other marketing efforts.
With all that in mind, let’s examine two central criteria that your website needs to meet before you start a CRO program.
Criterion #1: Revenue
Due to the cost involved in conducting CRO, revenue is the first qualifier. The reason is simple — to justify the often considerable investment in CRO, your revenue needs to grow higher than the cost of CRO.
Put simply, if you invested in something, you’d expect to receive more in return than the amount you invested.
Let’s do a quick calculation to illustrate this point:
Say you make $2 million in revenue, and you find that CRO can deliver a 10% increase on that number — netting you a $200,000 increase in total revenue. So spending $30,000 on CRO delivers an ROI of 567%.
Great! You’d get back more than 5x the amount of money you invested.
Lower revenues result in smaller ROIs, so it becomes harder to justify the cost of CRO, or requires a larger increase in conversions and revenue to deliver the same ROI.
This is why we can set the revenue threshold at $2,000,000 annually or more to achieve the best results from CRO.
Criterion #2: Traffic
Unless you have sufficient traffic to support research and experimentation, your website is not ready for CRO.
If you get 100,000 monthly unique visitors or more, with at least a 1% conversion rate — or 1,000 transactions — then CRO research can yield meaningful results.
Due to the statistical requirements of A/B testing, and the number-crunching nature of most research necessary to formulate viable tests, traffic lower than this threshold will severely limit the speed at which you can conduct tests, and undermine the confidence in the results of that research.
The speed at which tests can be deployed and reach significant results is called test program velocity. The more traffic a site has, the higher its possible testing velocity.
The more traffic a site has, the higher its possible testing velocity.
While conducting tests with less traffic is possible, they will likely take too much time to be effective. Why? A/B testing tools operate by leaving a cookie on the client computer. If the test lasts for long periods (generally, more than one month), there is a risk that the cookie will be deleted. This will invalidate your test results.
It’s also generally believed that the most effective results are achieved by a testing program that’s able to conduct at least 4 meaningful tests a month.
Specific types of A/B tests, such as multivariate and bandit testing, require even more traffic than regular A/B tests. Conducting bandit-type tests requires traffic upward of 200,000 – 300,000 unique visitors per month, and multivariate testing requires even more.
If the site does not fulfill these criteria, conversion research generally consists of setting up analytics and other quantitative data collection tools. Heuristic research and qualitative research are also viable options, though sites with a very small amount of traffic cannot be confident in findings obtained this way.
The best bet for smaller sites is to implement best practices and acquire more traffic to cross the viable threshold for conducting proper CRO. Best practices are the accepted standards of website design and content. A pretty comprehensive list can be found here.
While best practices are useful, never assume that they will automatically work for your website. Always take into account the specifics of your situation before applying any of these. We will reflect on those a bit more before we conclude this article.
An important note
CRO is not mutually exclusive with SEO. In fact, properly implemented, your CRO methodology will go hand-in-hand with your SEO efforts.
By using your CRO research results to base your SEO on your target audience’s demographics and characteristics, you’ll be able to do a much better job of targeting the right audience. Furthermore, many of the improvements that CRO makes to the content of your website will also make the site more SEO-friendly.
Instead of an SEO replacement, CRO should be considered an SEO multiplier.
Here is the entire rationale of CRO condensed to a single line: “Properly conducted CRO leads to a positive feedback loop for your business.”
What this means is through an organic increase in revenue that leads to greater profitability, you can increase your budget for traffic acquisition. An increased number of visitors grows your revenue even more, allowing for another round of increase in revenue.
This self-reinforcing loop creates a competitive edge, and ideally leads to ever-increasing profitability:
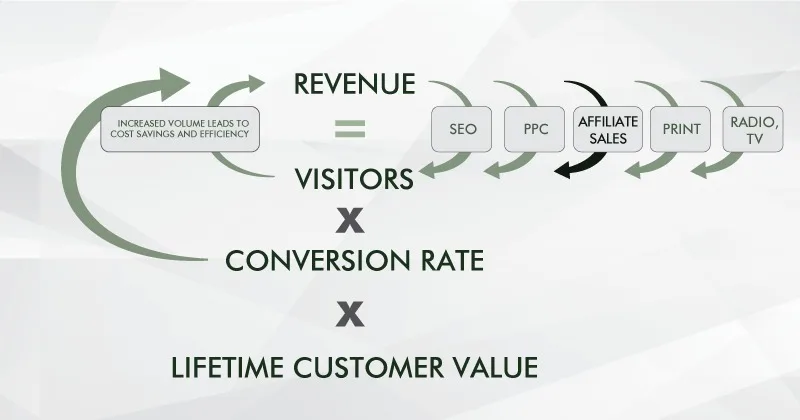
The self-perpetuating circle of CRO
A dilemma: In-house or outsourced CRO?
As with everything in business, you have two basic choices when assigning CRO efforts. You can either outsource the job to a CRO agency, or develop in-house capability. Both options come with certain advantages and disadvantages.
Outsourcing is a better choice when you haven’t already done any CRO work, and your company lacks experience with it.
By using an outside agency, you’ll have the reassurance of working with an experienced team, learning from them, and gaining the valuable know-how you’ll need to establish your own team. Many agencies target precisely this outcome with clients.
Outsourcing is also the most time-effective option. Experienced researchers and CRO practitioners will likely spot and solve issues on your website faster.
The disadvantage of hiring an agency is that, being outsiders, they may take some time to get to know your business. Implementation of changes also tends to be slower, as the process of implementing new designs will invariably include an approval stage.
Creating an in-house team from scratch is often an ecommerce business’ second choice. While in-house capability is what all growing ecommerce sites should aim for in the long term, going into CRO from scratch requires a lot of time and effort.
Finding the right people and hiring them can be hard, and identifying appropriate staff without already having done some CRO work can be impossible. Without prior experience, an in-house team may not do the job efficiently. Furthermore, their inexperience may inadvertently cause an additional cost in tools, since they may select options and features not necessary for the job (but which sound good). There is also the cost of training to consider.
However, there are significant advantages to forming an in-house team.
Any experience they gain and the results they achieve will remain privy to the company, and you’ll be able to use that knowledge in your other departments.
Your in-house team will have much greater motivation to achieve the best possible results. And finally, they will already be familiar with company culture and business practices.
As you can see, both approaches have merits and issues, and choosing between them is not easy. Both approaches also require a significant investment in tools, which adds to the overall cost.
Most likely, a combination of these two approaches will serve you best.
Now, let’s dive into how to do research for your CRO efforts.

Edin Šabanović is a senior CRO consultant working for Objeqt. He helps e-commerce stores improve their conversion rates through analytics, scientific research, and A/B testing. Edin is passionate about analytics and conversion rate optimization, but for fun, he likes reading history books. He can help you grow your ecommerce business using Objeqt’s tailored, data-driven CRO methodology. Get in touch if you want someone to take care of your CRO efforts.